Исследование посадочного удара самолета с шасси на воздушной подушке

Пневматические оболочки широко используются в различных сферах деятельности – в строительстве, на транспорте, в медицине.

Часто пневматические оболочки используются в качестве ограждения зон повышенного давления. Например, для судов на воздушной подушке (СВП) область повышенного давления – воздушная подушка – ограждается по бокам пневмоскегами, представляющими собой мягкие пневматические оболочки низкого давления, прикрепленные к жесткому днищу судна.

Статика и динамика пневмоскег изучена в настоящее время далеко не в полной мере. Неисследованными являются вопросы:

степень шероховатости опорной поверхности действующая на нормальную силу в пневмоскеге;

действие материала пневмооболочки на внешние силы;

действие (особенно в динамике) зоны повышенного давления на форму пневмооболочки и т.п.

В данной работе разбиваем задачу на 3 этапа:

1) Влияние трения на нормальную силу обжатого пневмоскега.

2) Копровый удар (вертикальный, посадочный) самолета с шасси на воздушной подушке.

3) Исследование посадочного удара самолета с шасси на воздушной подушке с учетом международных норм летной годности FAR 23. Аппарат приземляется на поверхность (вода) под углом не больше 6-ти градусов.

Согласно нормам FAR 23 максимальная, избыточная перегрузка при посадочном ударе коммерческих самолетов не должна превышать 3х единиц, при грубой посадке характеризуемой максимальной величиной вертикальной скорости -3.

Рассмотрим пневматическую оболочку, прикрепленную к жесткой платформе. Будем считать, что длина пневмооболочки много больше ее поперечных размеров (рис.1a).

a) Y

Платформа X

O

Z

PАТМ + P11

Ратм

Пневмооболочка

рис. 1

Будем также считать, что различные поперечные сечения пневмооболочки находятся в одинаковых условиях и форма этих сечений по длине (по оси Oz) не меняется, а материал, из которого сделана пневмооболочка, является нерастяжимым. Пусть в оболочку закачена некоторая масса воздуха, а внешнее давление равно атмосферному (рис1.). Будем считать, что в этом случае величина давления в оболочке известна:

Pабс = PАТМ + P11, (1)

где Pабс – абсолютное давление в пневмооболочке, РАТМ - атмосферное давление, Р11 – избыточное давление в оболочке.

Будем считать заданным:

1)длину нити ABCD (l0=0,965).

2)координаты точек A и B (из этого следует, что нам известна ширина зоны крепления AB).

3)начальное давление внутри пневмооболочки (Р1) и справа от нее (Р2).

4)коэффициент трения при соприкосновении с поверхностью.

5)величина обжатия пневмооболочки.

Требуется определить центральные углы пневмооболочки (φ1и φ2), радиусы (r1 и r2), координаты центров тяжести (Xo1 и Xo2), длину оболочки (dl) и нормальную силу, а так же осуществить подборку давления при заданном втором давлении. Говоря простым языком, требуется найти геометрию пневмооболочки.

Для решения задачи возьмем данные, рассмотренные в пункте 1. При выводе уравнений равновесия будем использовать аксиомы механики. Согласно принципу отвердевания, равновесие деформируемого тела не изменится, если тело считать абсолютно твердым. Очевидно, если нить ABCD находится в равновесии, то в равновесии будет находиться и каждый элемент этой нити. Мысленно выделим из нити ABCD элемент длиной l, и будем считать длину выделенного элемента бесконечно-малой. Со стороны отброшенных частей нити на элемент действуют силы T1 и T2; эти силы действуют в соответствии с другой аксиомой механики, которую называют аксиомой связей. По аксиоме связей, любое несвободное материальное тело можно считать свободным, если отбросить связи, наложенные на тело, и заменить их действия реакциями связей. Кроме того, на выделенное тело действует давление воздуха, складывающееся из двух сил: внутренней силы давления со стороны воздуха, находящегося в оболочке, и внешней силы давления со стороны воздуха, находящегося вне оболочки (рис.2).

T2 φ/2 Y1

φ/2

φ/2

P1абс

O T1

P

P2абс

рис.2

Так как длина выделенного элемента бесконечно мала, то можно считать, что форма этого элемента представляет собой дугу окружности неизвестного радиуса и центра. Тогда длина выделенного участка будет равна:

l = rφ. (3)

Внешнее и внутреннее давление действует перпендикулярно l (по радиусу) и, по длине l давления сводятся к силе Р, приложенной в центре элемента и направленной по радиусу (параллельно оси Oy1)

P = (P1абс – P2абс)rφ. (4)

Рассматриваемый элемент считается абсолютно твердым, поэтому действующие на него силы можно перемещать вдоль их линии действия. Линии, по которым действуют силы T1, T2, P, пересекаются в точке О. Такие системы сил называют сходящимися. Твердое тело, на которое действует система сходящихся сил, будет находиться в равновесии, если векторная сумма всех сил будет равна нуль или, что-то же самое, сумма проекций на каждую ось выбранной системы координат будет равна нулю.

Проецируем силы на оси системы координат Ox1y1:

Ox1: , (5)

Ox2: . (6)

Из уравнения (5) получаем T1 = T2, т.е. сила натяжения в рассматриваемом случае постоянна вдоль длины нити. Угол φ мал, т.к. длина l очень мала, значит sinφ ≈ φ. Тогда из уравнения (6) с учетом (4) и (5) имеем:

T = (P1абс – P2абс)r = const. (7)

Из (7) следует, что если избыточное внешнее давление отсутствует, или постоянно вдоль по длине нити, то поперечное сечение пневмооболочки представляет собой круговой элемент.

Так как абсолютное давление определяется по формуле (1), то из (7) для рассматриваемой задачи получаем:

. (8)

В рассматриваемой задаче нить находится под действием трех характерных зон избыточного давления: зоне BC с давлением P1 соответствует радиус r1 (рис.3); зоне обжатия CD, с избыточным нулевым давлением соответствует отрезок прямой CD (или дуга окружности бесконечно-большого радиуса); зоне DA с избыточным давлением (P1 – P2) соответствует радиус r2. При этом r2>r1.

Таким образом, кривая ABCD состоит из фрагментов двух окружностей радиусов r1 и r2 , и прямой CD; в точках C и D происходит скачок давлений, и в этих точках дуги должны гладко сливаться с прямой CD. Гладкий переход возможен только тогда, когда центры дуг окружностей O1 и O2 находятся на одной вертикали соответственно с точками С и D, т.е.

Xo2 = XB,(9)

Xo1 = XC.

Обозначая, через φ1 и φ2 центральные углы дуг из геометрии имеем:

r1(1 – cosφ1) = H + YB, (10)

r2(1 – cosφ2) = H + YA, (11)

Xo1 = XB + r1sinφ1, (12)

Xo2 = XA – r2sinφ2. (13)

Условие растяжимости нити дает еще одно уравнение:

(14)

где ТЕ – модуль упругости (100000 н/м). При ТЕ→∞ получаем частный случай, условие не растяжимости нити:

r1φ1 + r2φ2 + Xo2 – Xo1 = l0.

В дальнейшем будем считать, что нить растяжима.

Объединяя уравнения (8), (10), (11), (12), и (13), а также уравнения (2) и (3), получаем систему из 7 нелинейных алгебраических уравнений относительно неизвестных φ1, φ2, r1, r2, P1 и S:

P1r1 + P1f(Xo2 – Xo1) = (P1 – P2)r2, (15.1)

r2(1 – cosφ2) = H + YA, (15.2)

r1(1 – cosφ1) = H + YB, (15.3)

(15) Xo1 = XB + r1sinφ1, (15.4)

Xo2 = XA – r2sinφ2, (15.5)

(15.6)

(РАТМ + Р1)(S0L)n = (PАТМ + P2)(SL)n , n=1,4 (15.7)

Проанализируем систему (15). Если площадь S, ограниченная ABCD и AB, определяемая уравнением (16), известна, то при заданном P11 из последнего уравнения системы (15) легко определить давление в оболочке (это будет показано ниже) P1 . Вместе с тем давление P11 не входит в первые 6 уравнений системы (15). Это позволяет разделить задачу. В самом деле, если считать P1 заданным, решим первые 6 уравнений системы и далее, используя уравнение (16), построим процедуру определения P1 исходя из необходимого удовлетворения уравнения (15.7).

Первые шесть уравнений имеют вид:

P1r1 + P1f(Xo2 – Xo1) = (P1 – P2)r2; (a)

r2(1 – cosφ2) = H + YA; (б)

r1(1 – cosφ1) = H + YB; (в) (17)

Xo1 = XB + r1sinφ1; (г)

Xo2 = XA – r2sinφ2 (д)

(е)

После исключения Xo1 и Xo2 получаем:

r1φ1 + XA – r2sinφ2 – XB – r1sinφ1 + r2φ2 = l0

Выражая из уравнения (17 б, в)

,

и подставляя выражения r1 и r2 в уравнения, имеем:

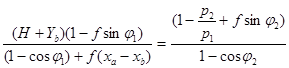(I)

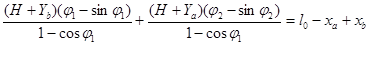
Получили систему (I), состоящую из двух нелинейных алгебраических уравнений с двумя неизвестными j1 и j2.

Обозначим первое уравнение системы (I) за f1(φ1,φ2) = 0, а второе за f2(φ1,φ2) = 0. Затем дифференцируем функции f1 и f2 по φ1 и φ2. Полученные производные подставляем в уравнения на шаге:

.

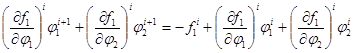
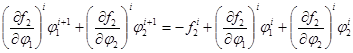Проведенный анализ системы показал, что аналитического решения построить не удается. Поэтому решение задачи осуществляется численно.

Численное решение задачи организовано следующим образом. Задавая начальное приближение избыточного давления в пневмооболочке P1(1) и, решая нелинейную систему (I), определяем геометрические характеристики поперечного сечения (j1, j2, r1, r2, Xo1, Xo2, dl, N). Далее, по найденным геометрическим характеристикам, определяем площадь поперечного сечения по формуле:

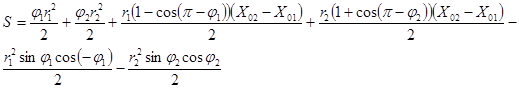. (16)

и используя, на основании закона сохранения массы воздуха, предварительно закаченного в пневмооболочку, уравнение:

(PАТМ + P1)(S0L)n=(PАТМ + P2)(SL)n (2)

(где n – показатель адиабаты (для воздуха n=1,4), L – длина оболочки, S0,S – площади, ограниченные нитью ABCD и платформой AB в начальном и исследуемом состоянии) находим откорректированное значение P1(2) . Если разность по абсолютной величине между P1(1) и P1(2) меньше некоторого числа d, где d - заданная величина, то значения, полученные при этом решении, будем считать конечными. Если условие не выполняется, то решаем все заново с новым значением P1(1) и т.д.

• Метод половинного деления
• Исследуем приземление самолета с шасси на воздушной подушке