Метод половинного деления

Y

C0 A

0 B C X

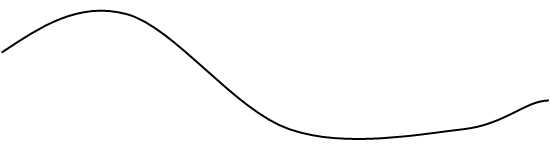
рис.3

Это один из надежных методов решения нелинейных уравнений. Он состоит в следующем. Допустим, что нам удалось найти отрезок [A , B] , в котором расположено искомое значение корня x=C, т.е. A<C<B (рис.3). В качестве начального приближения корня С0 принимаем середину этого отрезка, т.е. . Далее исследуем значение функции F(x) на концах отрезков [A , C0] , [C0 , B] , в точках A , C0 , B . Тот из них, на концах которого F(x) принимает значения разных знаков, содержит искомый корень, поэтому его принимаем в качестве нового отрезка. Вторую половину отрезка [A , B] на которой знак F(x) не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка и так далее. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, т.е. после n итераций он сокращается в 2n раз.

Для решения системы

Пусть нам дана система нелинейных алгебраических уравнений

φ1=¦1(φ1,φ2)

φ2=¦2(φ1,φ2).

Для нахождения корней φ1 и φ2 этой системы часто пользуются методом простой итерации

φ1(n+1)=¦1(φ1(n),φ2(n)),

φ2(n+1)=¦2(φ1(n),φ2(n)), где n=0,1,2,…

Надо заметить, что если процесс итерации сходится, то предельные значения

φ1=limφ1(n),

n®¥

φ2=limφ2(n).

n®¥

обязательно являются корнями системы.

Для решения уравнения

Для его использования исходное уравнение записывается в виде:

x = F(x).

Пусть известно начальное приближение корня x=c0. Подставляя это значение в правую часть уравнения получаем, новое приближенение:

c1 = F(c0).

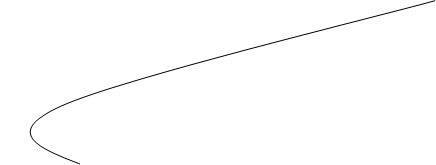
Далее, подставляя каждый раз, новое значение корня в уравнение получаем последовательность значений (рис.4):

cn+1 = F(cn), n = 1,2,…

Достаточным условием сходимости метода простой итерации является условие:

Y

N2

N1

N0 С2

C1

O C0 X

рис.4