Исследуем приземление самолета с шасси на воздушной подушке

Тогда еще раз учитывая (*)

Подставляем в (Δ)

Или, окончательно

Система уравнений оболочки до контакта (квазистатика).

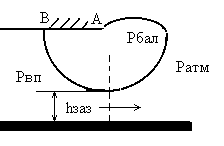
В первом приближении считаем, что до контакта оболочка характеризуется только двумя зонами: зоной действия давления со стороны ВП и внешней зоной, где действует атмосферное давление.

Тогда форма поперечного сечения оболочки представляет собой две дуги окружности неизвестного радиуса и центра.

Касательные внешние силы отсутствуют, следовательно

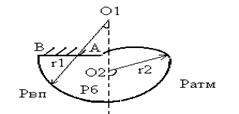
(3.1) – условия постоянства сил натяжения по длине поперечного сечения оболочки.

(3.2)

(3.3)

(3.2),(3.3) – геометрические условия склейки дуг.

(3.4)

(3.4) – линейная связь между внутренними силами и удлинением поперечного сечения оболочки.

– раскройная длина поперечного сечения.

– приведенный модуль упругости материала.

Уравнение для давления в оболочке выводится из условия постоянства массы закаченного в оболочку воздуха в предположении его адиабатического состояния.

(3.5)

– начальное, избыточное давление в оболочке, когда она представляет собой круговой сегмент (задается).

– начальная площадь поперечного сечения (задается).

– текущее давление в оболочке.

– текущая площадь поперечного сечения.

В необжатом состоянии:

Т.о. система уравнений необжатой (до контакта) оболочки имеет вид:

,

,

(3) ,

,

.

и 2. (уравнения движения и расхода) – дифференциальные, поэтому систему нелинейных алгебраических уравнений целесообразно представить в дифференциальном виде.

Дифференцируя все уравнения по t имеем:

3.1)

3.2)

3.3)

3.4)

3.5)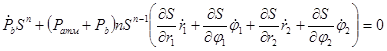

С учетом уравнений (1) и (2) получается система из 7 дифференциальных уравнений. Её надо привести к нормальному виду.